Obsah
Diferenciace a integrace jsou rovnice obsahující deriváty. Posledně jmenované, pokud se budete držet matematických vlastností, se rozdělí na běžné a soukromé. Deriváty představují rychlost změny a diferenciální rovnice popisuje vztah mezi veličinou, která se v procesu řešení neustále mění a vytváří nové proměnné.
Univerzitní profesor se snadno orientuje ve složitých operacích s integrály, převádí je na jeden celek a poté prokáže počet inverzní metodou. Schopnost rychle si pamatovat podrobnosti složitých vzorců však není k dispozici každému člověku, proto se doporučuje obnovit paměť nebo objevit nový materiál.
Význam a základní aplikace
Ve vědecké literatuře je derivace definována jako rychlost náchylná k transformaci funkce na základě jedné z jejích proměnných. Diferenciace je entita počtu, kterou lze porovnat se začátkem vyhledávání tečny k bodu. Jak víte, ten druhý má různé druhy a vyžaduje výpočetní vzorce pro vyhledávání. Předpokládejme, že musíte najít sklon tečny k grafu v bodě P. Jak to udělat? Stačí nakreslit obloukový pás přes určený objekt a zvednout jej nahoru, dokud nedostaneme dělenou čáru.

Funkce f V X se nazývá diferencovatelná v bodě X = a, pokud derivace f `(a) existuje na každé notaci její oblasti. Ukážeme příklad:
f `(a) = lim(h=0) × f (A + h) - f (A) / h
Aby byla rovnice podrobena diferenciaci a integraci funkcí tak, aby její umístění bylo možné v kterémkoli bodě x, neměla by být přerušena. Po vytvoření schematického obrázku předem budete moci ověřit platnost tvrzení. Z tohoto důvodu je oblast f `(X) určena existencí jejích limitů.
Předpokládejme, že y = F (X) je funkce Z X, pak derivát f (X) je dán jako dy/dx. Je také definována jako lineární rovnice, kde je nutné najít potřebná data pro y.
Pokud však v prvním případě hledáme derivaci y, pak v následujícím případě musíme najít f (x) Z x.
d/dx × (f(x)) la nebo df / dx la
Proto označení rychlosti změny funkce f (x) vzhledem k X v bodě A, který leží na jeho povrchu.
Pokud je známa derivace f`, která je ve své doméně diferencovatelná, můžeme najít její hodnotu f. V integrálním počtu nazýváme F Anti-derivát nebo primitivní funkce f `. Metoda jeho výpočtu je známá jako antidiferenciace nebo integrace.
Druhy a formy
Rovnice s jedním nebo více termíny, která zahrnuje deriváty závislé proměnné nezávislým způsobem, je známá jako diferenciál. Jinými slovy, skládá se z mnoha číselných hodnot, běžných nebo soukromých, které procházejí změnami v procesu řešení.

Prozatím existují následující typy diferenciálních rovnic.
Obyčejné. Jednoduchá rovnost přímo závislá na proměnné:
dy/dx + 5x = 5y
Se soukromými deriváty:
dy/dx + dy/dt = x3-t3
d2y/dx2 – c2 × d2y/dt2
Vyšší koeficient. Tento druh se vyznačuje účastí v pořadí diferenciální rovnice, jak je ukázáno na příkladu níže, kde se rovná 3. Číslo je považováno za nejvyšší z přítomných:
d3y/dx2 + 5 × dy/dx + y = √x
Funkce mohou mít několik druhů, je však výhodné použít jednoduchou uvozovku s charakteristickými vzorci integrace a diferenciace.
y’ = dy/dx
y’’ = d2y/dx2
y’’’ = d3y/dx3
Lineární. Proměnná, která se objevuje v rovnici, je zvýšena na sílu jednotky. Graf tohoto typu funkce je obvykle přímka. Například (3x + 5), ale (x3 + 4x2) není tohoto typu, protože vyžaduje jiné řešení.
dy/dx + xy = 5x
Nelineární. Jakákoli integrace a diferenciace řad s duálními způsoby, jak získat rovnost, se týká daného druhu:
d2y/dx2- ln y = 10
Metody rychlého získání výsledku
Nestačí zvážit formu, abyste pochopili, jak se vypořádat a uvést do praxe získané znalosti. V současnosti existuje několik způsobů řešení diferenciální rovnice.

To:
- Rozdělení proměnné. Provádí se, když lze příklad vykreslit jako dy / dx = f (y) g (x). Zvláštností je, že F A G jsou funkce patřící k jejich hodnotám. Díky tomu by měl být úkol převeden: 1 / f(y) dy = g (x) dx. A teprve poté přejděte na další položku.
- Metoda integračního faktoru. Používá se, když je příklad dy / dx + P(x) y = q(x), kde P A q jsou funkce pouze x.
Diferenciální výpočty prvního řádu vypadají jako y` + P (x) y = Q (x), protože obsahují potřebné funkce a derivát y. Následné zvýšení názvu funguje na stejném principu. Například deriváty neznámé funkce se mohou ukázat jako soukromé i běžné.
Nedefinované integrály
Pokud máte při jízdě na kole rychlost, podle času - můžete vypočítat ujetou vzdálenost pomocí údajů o strávených minutách? Tento úkol vypadá jako ohromující břemeno, ale integrály vám pomohou vyrovnat se s těmito vlastnostmi co nejefektivněji a získat výsledek.
Literatura faktu zdůrazňuje, že J ou odvrácenou stranou diferenciace. Integrace je skutečně metoda přidávání věcí. Spojuje částice mezi sebou a vytváří něco nového-celek. Hlavní věc v jakémkoli podobném příkladu: najděte nedefinované integrály a ověřte výsledky integrace diferenciací. To pomůže vyhnout se zbytečným chybám.
Pokud se chystáte hledat oblast jakékoli náhodné křivky, například y = F(x), použijte danou metodu. Pamatujte, že pouze všímavost vás zachrání před chybou.
Vzorce pro řešení
Po seznámení se základním konceptem diferenciace a integrace-zpětného výpočtu prostřednictvím funkcí je tedy třeba stručně zvážit některé základy. Jsou uvedeny níže.

Základní pravidla výpočtu
Integrované funkce jako f (x) lze snadno přeložit do rovnosti, pokud je rovnice reprezentována jako: ∫ f(x) dx = F(x) + C.
Zde se F (x) nazývá anti-derivát nebo primitivní. f (x) - integrální funkce. dx-působí jako další číselný agent. C-integrovaná nebo libovolná konstanta. x-vyčnívá podle strany rovnosti.
Z výše uvedeného tvrzení lze odvodit, že integrace a diferenciace řad jsou dva protichůdné procesy. Společně fungují jako jeden z typů operací zaměřených na získání konečného výsledku provedeného nad samotnou rovnicí.
Nyní, když víme více o vlastnostech počtu, je vhodné zdůraznit preferenční rozdíly, nezbytné pro další porozumění:
- Diferenciace a integrace jsou schopny současně splnit pravidla linearity.
- Operace jsou zaměřeny na nalezení co nejpřesnějšího řešení, předpokládají však omezení pro jejich určení.
- Při diferenciaci polynomiálního příkladu je výsledek o 1 menší než stupeň funkce, zatímco v případě integrace je získaný výsledek převeden na jiný a jedná podle opačného schématu.
- Dva druhy řešení, jak bylo dříve řečeno, jsou proti sobě. Vypočítávají se podle vzorců integrace a diferenciace.
- Derivace jakékoli funkce je jedinečná, ale na druhé straně se dva integrály v jednom příkladu mohou lišit konstantou. Právě toto pravidlo představuje hlavní složitost při provádění úkolů.
- Při jednání s deriváty můžeme uvažovat o derivátech v bodě. Téměř stejně jako v integrálech poskytují funkce v intervalu.
- Geometricky derivace popisuje rychlost změny velikosti vzhledem k druhé, zatímco neurčitý integrál představuje křivku. Je rozložen v paralelním směru a má také tečny během průsečíku nerovných čar s jinými ortogonálními k ose představující proměnnou.
Metody sčítání
Pokud narazíte na problém, jak se sumace používá pro matematické operace Diferenciace Integrace, měli byste se důkladně seznámit se základními vzorci. Jsou axiomem ve výuce, proto se používají všude. Všimněte si, při použití na vlastních příkladech, vzorce jsou správné, pouze pokud začínají i = 1.

Řešení "po částech"
Někdy funkce vyžaduje nestandardní přístup k dosažení konečného výsledku a splnění podmínek rovnosti. Integrovaná integrace a diferenciace řad je založena na identitě, která je vyjádřena: ∫ f(x) g’(x) dx = f (x) g(x) - ∫ f’(x) g(x) dx
Algoritmus dané techniky je následující:
- Vyjádřit integrovanou funkci jako produkt dvou výrazů. Označme jeden z nich f (x), druhý g ` (x).
- Nyní pokračujte v identifikaci dalších dvou vzorců, které lze použít při provádění první položky. Řada se změní. Diferenciací převedeme f `(x), abychom získali výrazy f (x). Pokračujeme do jiné části - G (x) se integruje do g`(x). Přitom DX zůstává v původní podobě a nepoužívá se.
- Vložte výsledné výrazy do vzorce po částech. Postup zde končí a nyní se můžete pokusit vyhodnotit nový integrál vpravo, protože je mnohem snazší pochopit.
Dříve data metoda zahrnovala integrace po částech pomocí matice. Metoda byla úspěšná, ale trvala dlouho, proto se nyní používá méně často, ve zvláštních případech, kdy je řešení téměř nemožné najít. K tomu stačí umístit f A g `na první řádek a vypočítat f` A g na druhý.
Proč potřebujete integraci po částech?
Situace se dějí jinak. Někdy jsou řešení mnohem složitější než na první pohled. Proto je třeba zdůraznit hlavní problémy, které se často vyskytují s integrovanou integrací a diferenciací výkonových řad. Zvažte dvě základní pravidla.
Nejprve část, kterou hodláme integrovat, tj. Udělat to je důležité co nejvíce rychle. Faktem je, že komplexní integrace pro g zřídka vede ke zlepšenému integrálu, což zvyšuje složitost. To vše negativně ovlivňuje svobodu našich jednání během rozhodnutí a také závisí na stupních, sinusech a kosinusech. Nechte hledání správné odpovědi chvíli trvat, ale povede ke správnému než zmatenému.
Za druhé, všechno ostatní, to znamená část, kterou hodláme odlišit a označit F, by se po transformaci mělo znatelně odlišit. Po nekomplikovaném postupu si všimneme, že nový integrál bude jednodušší než předchůdce.

Když tedy zkombinujeme dvě pravidla a použijeme je při řešení, získáme příležitost využít diferenciaci a integraci výkonových funkcí, které mají smysl zvažovat po částech.
Existuje také způsob odstranění X, který umožňuje efektivní zapojení transformací v různých situacích. Například můžeme snadno integrovat vynásobením funkce polynomem, který redukujeme diferenciací.
∫ x2 sin(3x) dx
∫ x7 cos(x) dx
∫x4 e4x dx
Jako f bereme sílu x (obecněji polynom) a také používáme g`. Je zřejmé, že každá diferenciace snižuje stupeň čísla o jednu, protože pokud je v příkladu dostatečně vysoká, použijte čestnou integraci několikrát. To pomůže zkrátit čas.
Složitost některých rovnic
V tomto případě jde o diferenciaci a integraci výkonových řad. Na funkci lze pohlížet, jako by X-byla oblast intervalu konvergence bodů. Pravda, metoda nebude vyhovovat všem. Faktem je, že jakékoli funkce mohou být vyjádřeny jako mocenské řady, převedeny na lineární strukturu a naopak.
Například dáno ex. Můžeme to vyjádřit jako rovnici, která je ve skutečnosti jen nekonečným polynomem. Výkonová řada je snadno rozpoznatelná výpočtem, ale není vždy efektivní.
Určitý integrál jako limit součtu
Podívejte se na následující grafickou integraci a diferenciaci.

Aby bylo možné snadno porozumět složité funkci, stačí ji pečlivě pochopit. Odhadneme oblast PRSQP mezi křivkou y = f (x), osou X a souřadnicemi "x = a" A "x = b". Nyní rozdělte interval [a, b] na ` n ` stejných dílčích intervalů označených takto: [x0 , x1 ], [x1 , x2 ], [x2 , x3 ]…. [xn - 1 , xn ].
Kde x0 = a, x1 = a + h, x2 = a + 2h, x3 = a + 3h… .. xr = a + rh a xn = B = a + nh nebo n = (b-a) / h. (1). Všimněte si, že při n → ∞ H → 0.
Dotčený prostor PRSQP je součtem všech " n " subdomén, kde každý je definován na určité průměrnosti [xr-1 , xr ], r = 1, 2, 3… n. Se správným přístupem mohou být tyto funkce podrobeny diferenciaci a integraci pro rychlé řešení.
Nyní se podívejte na ABDM na obrázku. Na jeho základě je vhodné provést následující pozorování oblasti: (ABLC) < (ABDCA) < (ABDM).
Všimněte si také, že při h → 0 nebo Xr - xr-1 → 0 všechny tři oblasti se navzájem téměř rovnají. Proto máme:
sn = h [f(x0) + f(x1) + f(x2) + …. f(xn – 1)] = h r=0∑n–1 f(xr) (2)
nebo Sn = h [f(x1) + f(x2) + f(x3) + …. f(xn)] = h r=1∑n f(xr) (3)
V tomto případě sn a Sn označují součet ploch všech spodních a horních obdélníků zvednutých v intervalech [xr–1, xr] pro r = 1, 2, 3,..., N, resp. Abychom to uvedli do perspektivy, lze rovnici (1) přepsat jako:
sn< oblast oblasti (PRSQP) < Sn … (4)
Kromě toho se předpokládá, že mezní hodnoty (2) a (3) jsou v obou případech stejné a společná je pouze oblast pod křivkou. Nakonec máme:
limn → ∞ Sn = limn → ∞ sn = oblasti PRSQP = ∫ab f(x) dx … (5)
Plocha je také mezní hodnotou prostoru, který je mezi obdélníky pod křivkou a nad křivkou. Pro pohodlí následuje všimnout si na výšku obrázku rovnající se křivce na levém okraji každého dílčího intervalu. Rovnice je proto přepsána do konečné varianty:
∫ab f(x) dx = limn → ∞ h [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
nebo ∫ab f(x) dx = (b – a) limn → ∞ (1/n) [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
Závěr
Diferenciace a integrace se mezi sebou liší řadou vlastností, vzorců a opačných změn. Jeden nemůže být přeměněn na druhý bez pomoci. Pokud diferenciace pomůže najít derivaci, pak integrace provede úplně jinou akci. Přidává některé části, je schopna pomoci s tituly tím, že je zkrátí nebo zdokonalí příklad zjednodušením.
Platí také pro ověření diferencovaných rovnic. Jinými slovy-fungují jako jeden celek, který nemůže koexistovat samostatně, protože se navzájem doplňují. Použitím pravidel, znalostí mnoha technik, je nyní zaručeno, že vyřešíte složité problémy.
 Hranice provozní odpovědnosti: pojem, právní definice, formy dokumentů předpisy, články, komentáře a odpovědi na otázky
Hranice provozní odpovědnosti: pojem, právní definice, formy dokumentů předpisy, články, komentáře a odpovědi na otázky Tolerance v psychologii je... Pojem, definice, základní typy a psychologie vztahů
Tolerance v psychologii je... Pojem, definice, základní typy a psychologie vztahů Definice zorného pole: pojem, technika a indikace
Definice zorného pole: pojem, technika a indikace Pevná nabídka je... Pojem, definice a platnost
Pevná nabídka je... Pojem, definice a platnost Článek o nepravdivých obviněních: definice, pojem, nová pravidla, vlastnosti aplikace zákona a odpovědnost za jeho neplnění
Článek o nepravdivých obviněních: definice, pojem, nová pravidla, vlastnosti aplikace zákona a odpovědnost za jeho neplnění Capex je... Pojem, definice, výpočet výdajů a příklady
Capex je... Pojem, definice, výpočet výdajů a příklady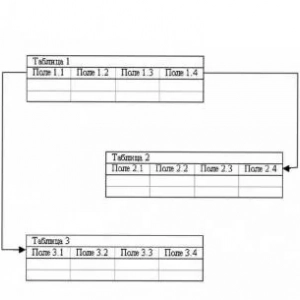 Relační datový model je... Definice, pojem, struktura a teorie normalizace
Relační datový model je... Definice, pojem, struktura a teorie normalizace Co je bod zlomu: pojem, definice a vzorec výpočtu s příklady
Co je bod zlomu: pojem, definice a vzorec výpočtu s příklady St. 16 std neplatnost smluvních podmínek, které porušují práva spotřebitele: definice, pojem, nová pravidla, vlastnosti aplikace zákona a odpovědnost za jeho nedodržení
St. 16 std neplatnost smluvních podmínek, které porušují práva spotřebitele: definice, pojem, nová pravidla, vlastnosti aplikace zákona a odpovědnost za jeho nedodržení